Realization of Wilson fermions in topolectrical circuits

Abstract

The Wilson fermion (WF) is a fundamental particle in the theory of quantum chromodynamics. Theoretical calculations have shown that the WF with a half skyrmion profile represents a quantum anomalous semimetal phase supporting a chiral edge current, but the experimental evidence is still lacking. In this work, we report a direct observation of the WF in circuit systems. We find that WFs manifest as topological spin textures analogous to the half skyrmion, half-skyrmion pair, and Néel skyrmion structures, depending on their mass. Transformations of different WF states are realized by tuning the electric elements. We further experimentally observe the propagation of chiral edge current along the domain-wall separating two circuits with contrast fractional Chern numbers. Our work provides experimental evidence for WFs in topolectrical circuits. The nontrivial analogy between the WF state and the skyrmionic structure builds an intimate connection between the two burgeoning fields.

Introduction

Lattice quantum chromodynamics is an effective method to study the strong interactions of quarks mediated by gluons^1,2. In lattice quantum chromodynamics calculation, quarks are represented by fermionic fields and placed at lattice sites, and gluons play the role of interactions between neighboring sites³. However, when naively putting the fermionic fields on a lattice, we will meet the fermion doubling problem⁴, i.e., the emergence of 2^d−1 spurious fermionic particles for each original fermion (d is the dimension of the spacetime). The origin of the doubling problem is deeply connected with chiral symmetry and can be traced back to the axial anomaly⁵. To remove the ambiguity, Kenneth Wilson developed a technique by introducing wave-vector-dependent mass, which modifies the Dirac fermions to Wilson ones⁶. The fermion doubling issue exists in condensed matter physics as well^7,8,9,10,11. It prevents the occurrence of quantum anomalies in lattices, such as the quantum anomalous Hall insulator¹⁰ and Weyl semimetal with single node¹¹. It is known that Dirac fermions manifest as the low-energy excitations of topological semimetals/insulators (e.g., graphene)^12,13,14,15. However, the observation of Wilson fermion (WF) is yet to be realized.

Recent works show that electrical circuits can be used to mimic and explore the properties of both bosons^16,17 and fermions^18,19,20. In this work, we utilize a lattice model to realize the WF and probe it in topolectrical circuit experiments^{20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39}. We find that the nontrivial state of the WF strongly depends on its mass and can be classified into three categories characterized by different Chern numbers of 0, ±1/2, and ±1, corresponding to the half-skyrmion pair, half skyrmion, and Néel skyrmion, respectively. We propose a circuit method to efficiently manipulate the transport and transformation of the WF states. In this system, the fractional Chern number dictates a quantum anomalous semimetal (QASM) phase with a chiral edge current as suggested in ref. ⁴⁰. Here, we report a direct observation of the chiral current along the domain wall (DW) separating two circuits with contrast fractional Chern numbers being 1/2 and −1/2. WFs in a three-dimensional (3D) circuit system are constructed as well. They are characterized by 3D winding numbers and accompanied by the emergence of the surface states and DW states at the boundaries. Our work opens the door for realizing the exotic WFs in solid-state systems.

Results and discussion

We begin from the Dirac Hamiltonian ${{{{{\mathcal{H}}}}}}=c{{{{{\bf{k}}}}}}\cdot \alpha +m{c}^{2}\beta$ with c the light speed, k the wave vector, and α, β being the Dirac matrices, which describes a Dirac fermion with the mass m⁴¹. Expressing this Dirac Hamiltonian on a lattice of the tight-binding form, we obtain ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{D}}}}}}}=\mathop{\sum }\nolimits_{i = 1}^{d}\frac{\hslash v}{a}\sin ({k}_{i}a){\alpha }_{i}+m{v}^{2}\beta$ with a the lattice constant and ℏv the hopping strength (d is the space dimension). It is straightforward to verify that 2^d − 1 non-physics fermion doublers appear at the Brillouin zone (BZ) boundaries k_i = π/a. Following Wilson’s method, we derive the WF Hamiltonian of the following form ${{{{{\mathcal{H}}}}}}={{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{D}}}}}}}+{{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{W}}}}}}}$ with ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{W}}}}}}}=\frac{4b}{{a}^{2}}{\sin }^{2}\frac{{k}_{i}a}{2}\beta$ being the k-dependent Wilson mass term⁴⁰. Here, the k-independent mass m in Hamiltonian ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{D}}}}}}}$ is referred to as the dispersionless mass of WFs. It is noted that the ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{W}}}}}}}$ term breaks the parity symmetry in two-dimensional (2D) and chiral symmetry in 3D cases, which can circumvent the fermion doubling problems⁴ and reproduce the quantum anomaly in the continuum limit. In Supplementary Note I, we show the details how the doublers from Dirac Hamiltonian are removed by introducing the Wilson mass term. Next, we report the realization of the Wilson Hamiltonian in electrical circuits.

Circuit model

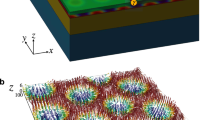
We consider a 2D spinful square lattice in Fig. 1a. The circuit is constituted by four types of capacitors ± C_1,2 and the negative impedance converters with current inversion (INICs) in Fig. 1b, where A and B parts correspond to the massless Dirac and Wilson mass Hamiltonians, respectively. It is noted that one can utilize inductors to replace negative capacitors because the admittance of the negative capacitor −iωC is equivalent to the inductor $-i\frac{1}{\omega L}$ for L = 1/(Cω²)⁴². Here, ω is the working frequency. We implement two sites to imitate a (pseudo-) spin, indicated by the red rectangle in Fig. 1a, b. The INIC is set up by an operational amplifier and three identical resistors R, as shown in Fig. 1c. In Fig. 1d, we show the realization of the staggered on-site potential, which is modeled as the dispersionless mass of WF.

Fig. 1: Two-dimensional model of Wilson fermions.

a Illustration of a 2D spinful square lattice. b The circuit realization of the hopping terms by A+B parts. Part A consists of two kinds of capacitors ± C₁ and the negative impedance converters with current inversion (INICs). Part B is composed of two types of capacitors ± C₂. The red rectangle indicates the correspondence between spin and circuit nodes. c Details of the INIC. The INIC is composed of an operational amplifier (OP) and three resistors R, acting as a positive (negative) resistor from right to left (left to right). d The realization of the staggered on-site potentials.

The circuit response is governed by Kirchhoff’s law $I(\omega )={{{{{\mathcal{J}}}}}}(\omega )V(\omega )$ with I the input current and V the node voltage. ${{{{{\mathcal{J}}}}}}(\omega ,{{{{{\bf{k}}}}}})$ is the circuit Laplacian written as

$${{{{{\mathcal{J}}}}}}(\omega ,{{{{{\bf{k}}}}}})=\left(\begin{array}{cc}{j}_{11}&{j}_{12}\\ {j}_{21}&{j}_{22}\\ \end{array}\right),$$

(1)

where ${j}_{11}=4i\omega {C}_{2}-2i\omega {C}_{2}(\cos {k}_{x}+\cos {k}_{y})+4i\omega \Delta {C}_{2},{j}_{12}=2iG\sin {k}_{x}+2\omega {C}_{1}\sin {k}_{y},{j}_{21}=2iG\sin {k}_{x}-2\omega {C}_{1}\sin {k}_{y},$ and ${j}_{22}=-4i\omega {C}_{2}+2i\omega {C}_{2}(\cos {k}_{x}+\cos {k}_{y})-4i\omega \Delta {C}_{2}$, with G = 1/R the conductance and Δ being the mass coefficient of WFs. In the presence of conductance, the time-reversal symmetry (${{{{{\mathcal{T}}}}}}$) of the system is broken because of ${{{{{\mathcal{J}}}}}}{(\omega ,{{{{{\bf{k}}}}}})}^{* }\ne -{{{{{\mathcal{J}}}}}}(\omega ,-{{{{{\bf{k}}}}}})$²⁷.

By expressing ${{{{{\mathcal{J}}}}}}(\omega )=i{{{{{\mathcal{H}}}}}}(\omega )$ with the Dirac matrices, we obtain

$${{{{{\mathcal{H}}}}}}(\omega )= 2G\sin {k}_{x}{\alpha }_{x}+2\omega {C}_{1}\sin {k}_{y}{\alpha }_{y}+4\omega {C}_{2}\left({\sin }^{2}\frac{{k}_{x}}{2}+{\sin }^{2}\frac{{k}_{y}}{2}\right)\beta +4\omega \Delta {C}_{2}\beta ,$$

(2)

where α_x, α_y and β represent the Pauli matrices σ_x, σ_y, and σ_z, respectively. It is noted that the above Hamiltonian fully simulates the lattice model of WFs. The first three terms in Eq. (2) represent the Hamiltonian of WF, and the last term is the dispersionless mass of WF. Meanwhile, by tuning the electric elements parameters G, C₁, and C₂, one can conveniently manipulate the shape of Wilson cones (similar to the Dirac cones).

In what follows, we analyze the topological properties of the lattice model.

Topological phase and phase transition

For a ${{{{{\mathcal{T}}}}}}$-broken 2D two-band system, one can evaluate the Chern number⁴³

$${{{{{\mathcal{C}}}}}}=-\frac{1}{2\pi }{\int}_{{{{{{\rm{BZ}}}}}}}\left(\frac{\partial {A}_{y}}{\partial {k}_{x}}-\frac{\partial {A}_{x}}{\partial {k}_{y}}\right)d{k}_{x}d{k}_{y},$$

(3)

to judge its topological properties. Here ${{{{{\bf{A}}}}}}({{{{{\bf{k}}}}}})=i \langle {u}_{{{{{{\bf{k}}}}}}}| {\nabla }_{{{{{{\bf{k}}}}}}}| {u}_{{{{{{\bf{k}}}}}}} \rangle$ is the Berry connection with $| {u}_{{{{{{\bf{k}}}}}}} \rangle$ the eigenstate of lower band.

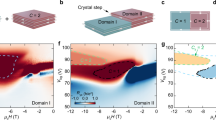
In following calculations, we adopt C_i = C = 1 nF (i = 1, 2), f = ω/(2π) = 806 kHz (In experiments, we will use L = 39 μH to replace −C, so we choose $\omega =1/\sqrt{LC}$), and G = ωC = 0.005 Ω⁻¹ (R = 200 Ω). Calculations of Chern number as a function of the dispersionless mass parameter Δ are plotted in Fig. 2a. We find the Chern numbers are quantized to five values ± 1, $\pm \frac{1}{2}$, and 0. It is noted that the Chern number is irrelevant to the value of C₁ but becomes opposite if C₂ changes its sign. We show the first BZ and typical band structures in Fig. 2b. Combined with the topological index, we classify these topological phases as follows. The band gaps open for the parameter intervals ① and ⑦, where the Chern number is zero. It gives the trivial insulator phase. For parameters in ② and ⑥, the band gaps close at M and Γ points, respectively. Surprisingly, the Chern numbers are quantized to ∓1/2, respectively. This phase is dubbed the QASM⁴⁰. For parameter zones ③ and ⑤, the band gaps open with the topological number ${{{{{\mathcal{C}}}}}}=\mp 1$, both of which represent Chern insulators with opposite chiralities. For the parameter region ④, the band structure closes at X point with a vanishing Chern number, indicating a normal semimetal phase.

Fig. 2: Topological indexes and Wilson fermions.

a The Chern number ${{{{{\mathcal{C}}}}}}$ steps as a function of the dispersionless mass Δ. The red stars and circle represent ${{{{{\mathcal{C}}}}}}=\pm \!\frac{1}{2}$ and ${{{{{\mathcal{C}}}}}}=0$, corresponding to quantum anomalous semimetal and normal semimetal phases, respectively. b The first Brillouin zone and the typical band structures for Δ = −2.5, −2, −1.5, −1, −0.5, 0, 0.5, respectively, corresponding to different parameter intervals in (a). The orange and blue curves indicate the two branches of band structures. c The spin textures of Wilson fermions in the momentum space.

By expressing Eq. (2) as ${{{{{\mathcal{H}}}}}}={{{{{\bf{f}}}}}}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\sigma }}}}}}$, one can define a unit spin vector $\hat{{{{{{\bf{f}}}}}}}({{{{{\bf{k}}}}}})$ as $\hat{{{{{{\bf{f}}}}}}}({{{{{\bf{k}}}}}})=\frac{{{{{{\bf{f}}}}}}({{{{{\bf{k}}}}}})}{| {{{{{\bf{f}}}}}}({{{{{\bf{k}}}}}})| }$, where f(k) = (f_x, f_y, f_z) is the coefficient of Pauli matrices and $| {{{{{\bf{f}}}}}}({{{{{\bf{k}}}}}})| =\sqrt{{f}_{x}^{2}+{f}_{y}^{2}+{f}_{z}^{2}}$. Figure 2c displays the spin textures of 2D WFs, which evolve as the increasing of dispersionless mass. The spin textures are reminiscent of the magnetic solitons in the condensed matter system^44,45,46. It is observed that the spin textures of trivial insulator, Chern insulator, QASM, and normal semimetal correspond to the ferromagnetic ground state, skyrmion, half skyrmion, and half-skyrmion pair, respectively. By evaluating the topological charge $Q=\frac{1}{4\pi }{\int}_{{{{{{\rm{BZ}}}}}}}\hat{{{{{{\bf{f}}}}}}}\cdot (\frac{\partial \hat{{{{{{\bf{f}}}}}}}}{\partial {k}_{x}}\times \frac{\partial \hat{{{{{{\bf{f}}}}}}}}{\partial {k}_{y}})d{k}_{x}d{k}_{y}$ in Fig. 2c, we identify an intimate connection with the Chern number as $Q+{{{{{\mathcal{C}}}}}}=0$. This finding thus establishes an interesting map between WFs and magnetic solitons in electrical circuits.

In the broad spintronics community, the manipulation of skyrmion motion is crucial for the next-generation information industry⁴⁷. Here, we propose a method to control the circuit skyrmion motion in momentum space. We first consider a skyrmion configuration with Δ = − 0.5. To generate a skyrmion propagation along k_x direction over a distance k₀, one can modify Eq. (2) to ${{{{{\mathcal{H}}}}}}(\omega )=2G\sin ({k}_{x}-{k}_{0}){\sigma }_{x}+2\omega {C}_{1}\sin {k}_{y}{\sigma }_{y}-4\omega {C}_{2}[\cos ({k}_{x}-{k}_{0})+\cos {k}_{y}+\frac{1}{2}]{\sigma }_{z}$, which can be recast as ${{{{{\mathcal{H}}}}}}(\omega )=2{G}^{{\prime} }\sin {k}_{x}{\sigma }_{x}-2{G}^{{\prime\prime} }\cos {k}_{x}{\sigma }_{x}+2\omega {C}_{1}\sin {k}_{y}{\sigma }_{y}-[4\omega {C}_{2}^{{\prime} }\cos {k}_{x}+4\omega {C}_{2}^{{\prime\prime} }\sin {k}_{x}+4\omega {C}_{2}(\cos {k}_{y}+\frac{1}{2})]{\sigma }_{z}$. Compared with the original Eq. (2), one merely needs to modify two hopping strengths (${G}^{{\prime} }=G\cos {k}_{0}$ and ${C}_{2}^{{\prime} }={C}_{2}\cos {k}_{0}$) and to add two extra hopping terms ($-2{G}^{{\prime\prime} }\cos {k}_{x}{\sigma }_{x}$ and $4\omega {C}_{2}^{{\prime\prime} }\sin {k}_{x}{\sigma }_{z}$). Variable resistors and capacitors can be conveniently adopted to realize these operations in circuit systems.

Quantum anomalous semimetals

To show the properties of QASM (Δ = 0 with ${{{{{\mathcal{C}}}}}}=\frac{1}{2}$), we consider a ribbon configuration with periodic boundary condition along $\hat{x}$ direction and N_y = 50 nodes along $\hat{y}$ direction. Figure 3a shows the admittance spectra, where the conduction and valence bands touch at k_x = 0. There is no isolated band in this admittance spectra, so the edge state is absent. Considering the Hamiltonian (2), one can define a velocity operator as $v=1/(i\hslash )[x,{{{{{\mathcal{H}}}}}}]=\frac{\partial {{{{{\mathcal{H}}}}}}}{\partial {k}_{x}}=2G\cos {k}_{x}{\sigma }_{x}+2\omega {C}_{2}\sin {k}_{x}{\sigma }_{z}$. The transverse current density then can be written as

$$j(y)=\mathop{\sum }\limits_{n}^{{\varepsilon }_{n} < \mu }\int[2G\cos {k}_{x}{\phi }_{n}^{{{\dagger}} }({k}_{x},y){\sigma }_{x}{\phi }_{n}({k}_{x},y)+2\omega {C}_{2}\sin {k}_{x}{\phi }_{n}^{{{\dagger}} }({k}_{x},y){\sigma }_{z}{\phi }_{n}({k}_{x},y)]d{k}_{x},$$

(4)

with ϕ_n(k_x, y) being the wave functions of the n-th band and the sum index n indicating the bands below the admittance μ. We plot the current density for different positions in Fig. 3b. It is found that the current density decays from the boundary nodes, and its values are opposite for the top and bottom edges. Consequently, the chiral edge currents constitute the bulk-edge correspondence of QASM^40,48. It is noted that the chiral current differs from the one in magnetic systems that originates from the chiral spin pumping effect induced by the topological structures in real space^49,50.

Fig. 3: Features of the quantum anomalous semimetal.

a Admittance spectrum of the ribbon geometry. b The current density distribution for two different “Fermi” levels slightly deviating from the admittance eigenvalue j_n = 0 Ω⁻¹ (dashed lines in (a). c The admittance spectrum with the inset showing the wave functions near j_n = 0 Ω⁻¹. d The impedance distribution of the sample. e The configuration of the circuit domain wall with ± 1/2 topological charges in light blue and green regions. f The admittance spectrum. Insets: The distribution of the wave functions and impedances. g The partial printed circuit board used in the experiment. h Experimentally measured impedance.

Then, we consider a 10 × 10 square lattice to study the finite-size effect. Diagonalizing the corresponding circuit Laplacian, we obtain the admittance spectra shown in Fig. 3c and the wave functions near j_n = 0 Ω⁻¹ in the inset of Fig. 3c. In our circuit, the impedance between the node a and the ground is computed by ${Z}_{a,{{{{{\rm{ground}}}}}}}={\sum }_{n}\frac{| {\phi }_{n,a}{| }^{2}}{{j}_{n}}$ with ϕ_n,a the wave function of node a for nth admittance mode, which reflects the features of wave functions near j_n = 0 Ω⁻¹ and can be measured readily^25,33. By comparing Fig. 3d and 3c (inset), we find that the impedance of each node against the ground exhibits almost the same spatial distribution to wave functions, and one does not find an edge state.

To demonstrate the bulk-boundary correspondence, we consider a one-dimensional DW with 10 × 11 “spins” (an extra column is set up for DW configuration), as shown in Fig. 3e, where the capacitor C₂ has a kink at the center of the sample, i.e., C₂ > 0 ( < 0) in the light blue (green) region. In this circumstance, the Chern number varies from 1/2 (left) to −1/2 (right). The eigenvalue and wave function of the bound state can be solved as J = 2ωC₁k_y and $\phi (x,y)=\frac{1}{\sqrt{2\pi }}{\chi }_{y}\sqrt{\lambda }\exp (-\lambda | x| +i{k}_{y}y)$ with ${\chi }_{y}=\frac{\sqrt{2}}{2}{(-i,1)}^{{{{{{\rm{T}}}}}}}$ and $\lambda =\frac{{C}_{1}}{| {C}_{2}| }+\sqrt{{(\frac{{C}_{1}}{{C}_{2}})}^{2}+{k}_{y}^{2}}$. The nonzero eigenvalue means the bound states do not localize at zero admittance. One can obtain the effective velocity of the bound state ${v}_{{{{{{\rm{eff}}}}}}}=\frac{\partial J}{\partial {k}_{y}}=2\omega {C}_{1}$, indicting the DW bound state propagating along $\hat{y}$ direction (see Supplementary Note 2). In Fig. 3f, we show the admittance spectrum with the insets displaying the wave functions and impedances, from which one can clearly see the bound state confined inside the DW. Here, we use the inverse participation ratio p = lg(∑_i∣ϕ_n,i∣⁴) of the system to characterize the localization properties of the wave functions^51,52, and the green dots indicate the localized state.

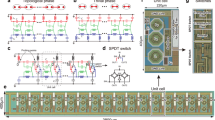
Then, we prepare a printed circuit board to verify the numerical results, as shown in Fig. 3g (see Methods for details). Figure 3h shows the experimental impedance distribution. It demonstrates a localized state between two domains, which compares well with the theoretical result in Fig. 3f. The existence of one bound state is closely related to the fact that the topological invariants between the two sides of the DW differ by 1. In addition, one cannot observe the edge states on the rest boundaries of the sample, which confirms that there is indeed no edge state. We also study the influence of the homogeneity of the circuit components on our results, which does not change our conclusion.

To show the chiral propagation of the bound state, we perform the circuit simulation with the software LTSPICE (http://www.linear.com/LTspice). By inputting a Gauss signal close to the DW, we observe the bound mode propagating along the $\hat{y}$ direction of DW. Finally, the voltage signal becomes a steady bound state inside the DW (see Supplementary Note 2).

Chern insulators and normal semimetal

To characterize Chern insulators (${{{{{\mathcal{C}}}}}}=\pm 1$), we compute the admittance for a ribbon configuration, with the results being shown in Fig. S3 of Supplementary Note 3. For the parameter Δ = −0.5 and −1.5, we find two crossing bands in the admittance gaps but with opposite charities. To show the chiral propagation of edge states, we perform the circuit simulation on a finite-size square lattice and observe a chiral voltage propagation (see Supplementary Note 3).

We note that at the phase transition point separating two Chern insulators (Δ = −1), the Chern number vanishes but the spin texture is still non-trivial. We consider a finite-size lattice with 10 × 10 “spins”. The admittance spectrum is plotted in Fig. 4a, showing that a series of localized states lie near j_n = 0 Ω⁻¹, and the corner states lying at nonzero admittance is caused by the open of band gap at phase-transition point (see Supplementary Note 4). The wave functions of localized states are displayed in the inset of Fig. 4a, from which we identify a corner state. The origin of the emerging corner states can be interpreted as the convergence of two Chern insulators with opposite chiralities, as shown by the green and black arrows in Fig. 4b. Due to the contrast of the chirality, the one-dimensional edge states can only accumulate at the sample corners, forming the zero-dimensional localized states, i.e., corner states. These corner states can be detected by measuring the distributions of impedance, as shown in Fig. 4c. If we consider circular samples with these parameters, the corner states will disappear for the circle with a large radius (smooth boundary) and the wave functions will concentrate on the convex right angle of the sample for a small circle (see Supplementary Note 5).

Fig. 4: The emergence of corner states.

a The admittance of the finite-size square lattice with 10 × 10 “spins” with the inset showing the wave functions near the admittance eigenvalue j_n = 0 Ω⁻¹. b The corner state formed by the convergence of Chern insulators with opposite chiralities. c Numerical impedance.

Three-dimensional Wilson fermions

As a nontrivial generalization, we consider a 3D hyper-cubic lattice with four sites in each cell, as shown in Fig. 5a. The hopping terms and on-site potentials are shown in Fig. 5b, c, respectively. One can write the circuit Laplacian as ${{{{{\mathcal{J}}}}}}(\omega )=i{{{{{\mathcal{H}}}}}}(\omega )$ with

$${{{{{\mathcal{H}}}}}}(\omega )= \, 2G\sin {k}_{x}{\alpha }_{x}+2\omega {C}_{1}\sin {k}_{y}{\alpha }_{y}+2G\sin {k}_{z}{\alpha }_{z} \\ +4\omega {C}_{2}\left[{\sin }^{2}\frac{{k}_{x}}{2}+{\sin }^{2}\frac{{k}_{y}}{2}+{\sin }^{2}\frac{{k}_{z}}{2}\right]\beta +4\Delta \omega {C}_{2}\beta ,$$

(5)

where α_x = σ_x ⊗ σ_x, α_y = σ_x ⊗ σ_y, α_z = σ_x ⊗ σ_z, and β = σ_z ⊗ σ₀ are Dirac matrices (see Supplementary Note 6).

Fig. 5: Three-dimensional circuit model of Wilson fermions.

a Three-dimensional hyper-cubic lattice model with four sites in each supercell. b The interactions between two cells along $\hat{x}$, $\hat{y}$, and $\hat{z}$ directions. c The realization of the on-site potentials.

The topological properties of the 3D system can be characterized by the winding number w₃⁵³. We find that the topological index w₃ can only take five quantized values, i.e., 0, $\pm \frac{1}{2}$, ± 1. For the topological insulator phase w₃ = 1, one can observe surface states. At the border of the two topological insulators with opposite winding numbers, we find the hinge states induced by the overlap of the surface states. For the QASM phase w₃ = 1/2, we observe the bounded surface state in a finite-size DW circuit along the $\hat{x}$ direction (see Supplementary Note 6).

Conclusions

To summarize, we experimentally observed WFs in circuit systems. In addition, we mapped WFs with different masses or configurations to magnetic solitons with different skyrmion charges, which will enable us to study the properties of skyrmions, half skyrmions, and half-skyrmion pairs in electrical circuit platforms. We showed that the nontrivial spin-texture of WFs in momentum space is fully characterized by Chern numbers and winding number in 2D and 3D systems, respectively. The chiral edge current associated with the QASM state dictated by a fractional Chern number was directly detected. Although we have measured the band structures of WFs and their topological boundary states, how to reveal the quasiparticle nature of WFs is still an open question. Our work presents the first circuit realization of WFs, which sets a paradigm for other platforms, such as cold atoms, photonic, and phononic metamaterials, to further explore these fascinating phenomena.

Methods

Experimental details

We implement the circuit experiment on a printed circuit broad shown in Fig. 6a. The circuit is composed of 10 × 11 cells, with each cell containing two nodes. The details of the circuit components are shown in the inset of Fig. 6a. Figure 6b displays the experimental instruments: DC power supply (IT6332A) and impedance analyzer (E4990A), which are used to provide the power for the operational amplifiers and measure the impedance over the sample, respectively.

Fig. 6: Experimental layout.

a The full image of the experimental printed circuit board. b The photos of the DC power supply and the impedance analyzer.

In Table 1, we list all elements used in our experiments, including the product companies, packages, mean values and their tolerances.

Table 1 Electric elements used in experiments.